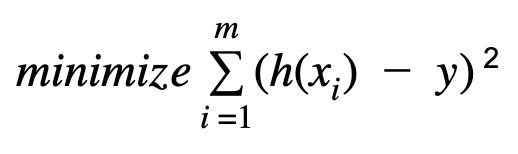Batch Gradient vs Stochastic Gradient Descent for Linear Regression

In this article, we will introduce about batch gradient and stochastic gradient descent method for solving the linear regression optimization problem. The linear regression problem frequently appears in machine learning. There are different ways of solving the linear regression optimization problem. The operation research methods uses the batch gradient descent, whereas the machine learning methods uses the stochastic gradient descent to solve the linear regression optimization problem. When we have millions of training examples, it might not be feasible to compute the gradient by using all the training examples as the system might run out of memory. Therefore, the stochastic gradient descent method is developed for machine learning problem to sample the training examples, compute the gradient in the sampled data and update the direction to find the optimal solution of the cost function.

Given the training examples of size m * n represented by pairs (x¹¹,x¹²,x¹³,…,y¹) (x²¹,x²²,x²³,…,y²), where each x represents the training example and y represents the corresponding labels of the training example. Let 𝝷¹, 𝝷²,… 𝝷^n be the parameters of the models then, the hypothesis of the linear regression is defined as follows:

h(xi) = 𝝷.X + b, where X is the m * n matrix of the coefficient and 𝝷 is the parameter of the model, whose value is obtained by solving the least square cost function.

The cost function for the linear regression is defined as :

The above cost function can be solved using the batch gradient and stochastic gradient descent method. The choice of batch vs stochastic gradient descent method depends on the value of m. If we have a large number of ‘m’, computing the gradient at each training example may not be feasible as it requires the substantial memory space. On the other hand, if the value of ‘m’ is small, we could use the batch gradient to solve the optimization problem.

The batch gradient descent could produce the better model than that by the stochastic gradient descent.The batch gradient converges faster than the stochastic gradient descent, and thus takes substantial lower time to train the model than that taken by the stochastic gradient descent. When we use the stochastic gradient descent, we often stop the training after the maximum number of iterations as converging to an optimal solution requires a substantially large number of iterations. This has the problem of early termination of the optimization algorithm and thus producing the sub-optimal model. On the other hand, the batch gradient descent converges to the optimal solution in fewer iterations and tends to produce the optimal solution of the cost function.

The choice of batch vs stochastic depends on the size of your problem. If you could load your data in the memory and compute the gradient, then we should use batch gradient instead of stochastic gradient descent for training the model. In many real-world applications, we end up with few number of data points in training even if the raw data has millions of rows. This is because we need to aggregate data to extract the data points for modeling and the aggregation often reduces the number of data points in the model. In such scenarios, we could load all data in the memory and batch gradient might give better model than the stochastic gradient descent method.